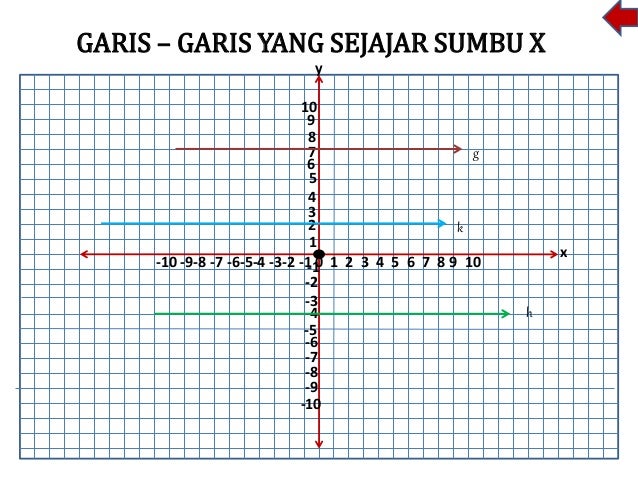
Tegak Lurus Dari Sumbu X
Latihan soal penilaian keterampilan kd 42 1.
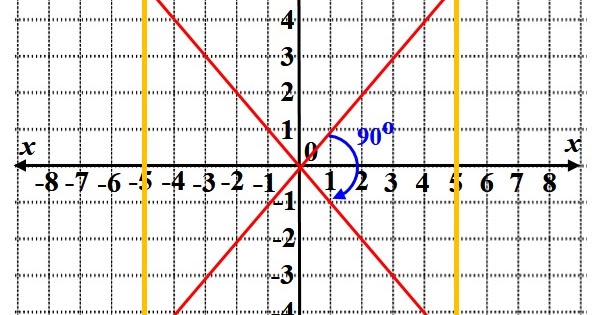
Tegak lurus dari sumbu x. Pengertian garis titik bidang dan ruang beserta contohnya a. Persamaan nya yakni sebagai berikut. Gradien dari dua persamaan garis tersebut ternyata saling berkebalikan negatif.
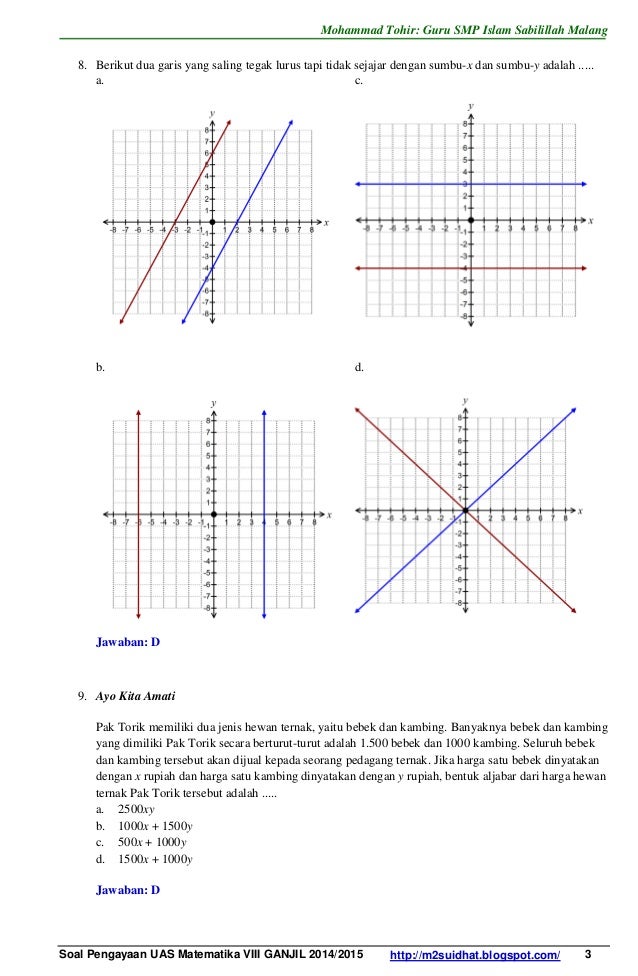
Gradien dua garis saling tegak lurus. Sebutkan garis garis yang memotong dengan sumbu x. Garis k melalui titik c3 0 dan d0 3.
Soal no1 tentukanlah. Jika kemiringan garis maka kemiringan garis. Untuk mencari gradien garis yang saling tegak lurus caranya sama dengan car yang di atas yaitu dengan menggunakan dua buah titik dari masing masing garis k dan i.
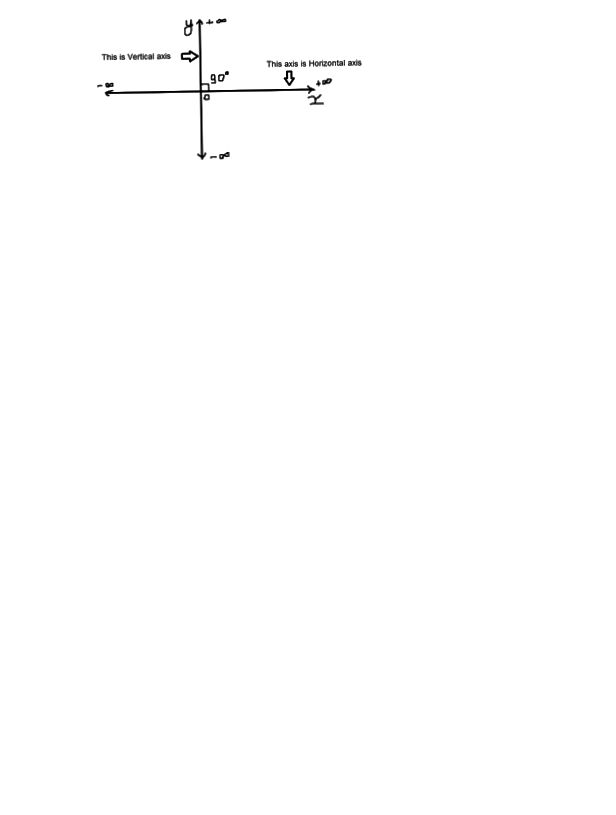
Maka jika l adalah sebuah garis tegak lurus dengan garis p maka berlaku ml mp 1. Sumbu horizontal akan diberi label x dan sumbu vertikal diberi label y. Misalkan garis hijau dan garis coklat tersebut saling tegak lurus satu sama lain.
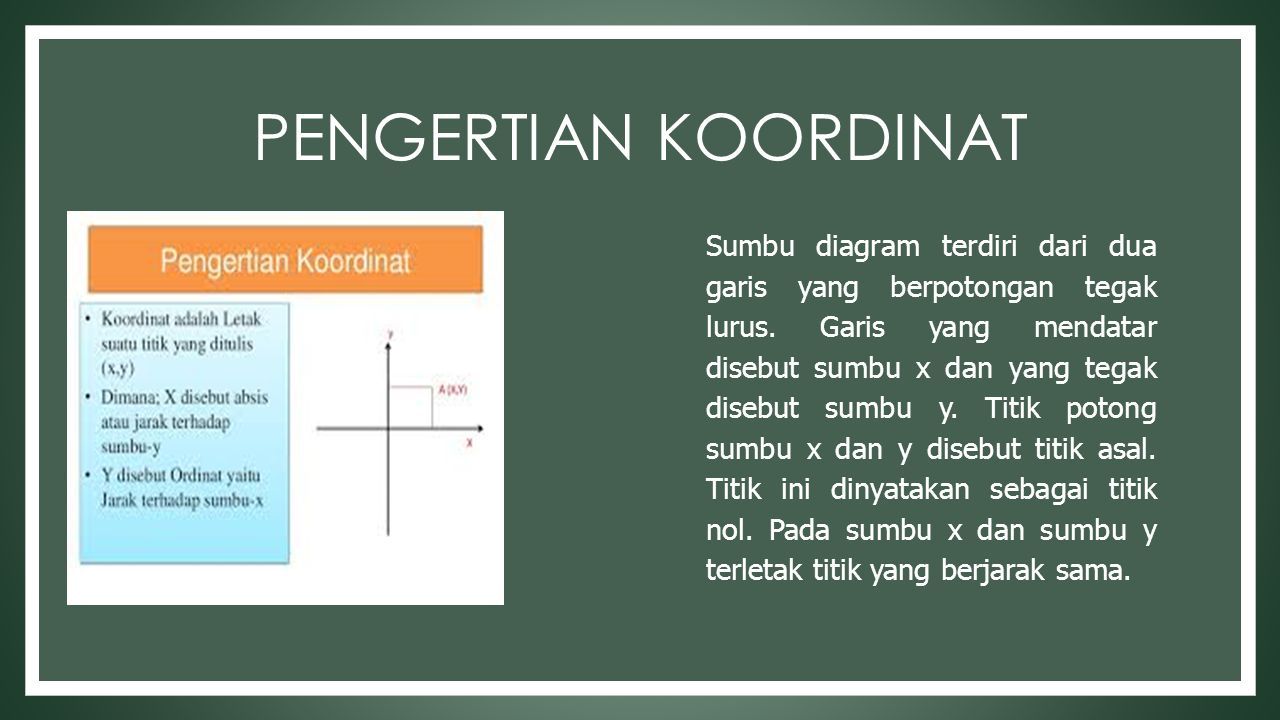
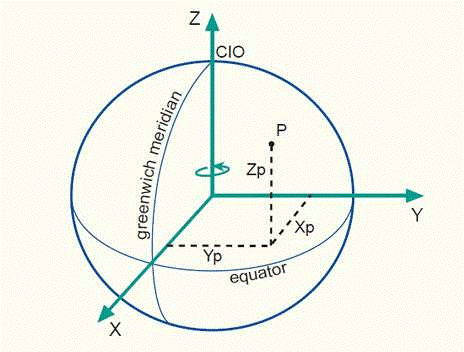
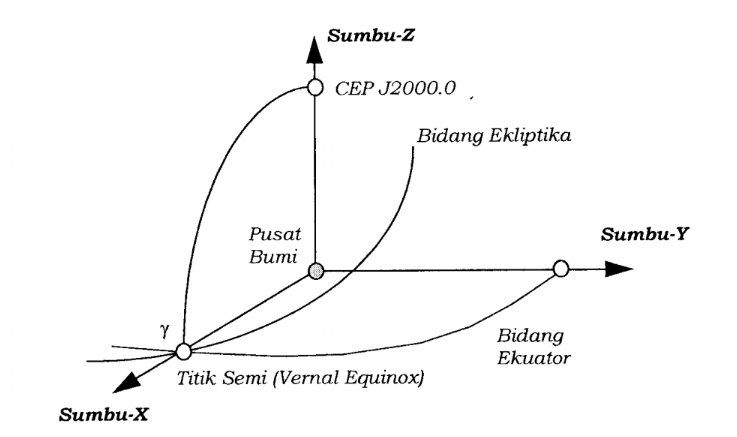
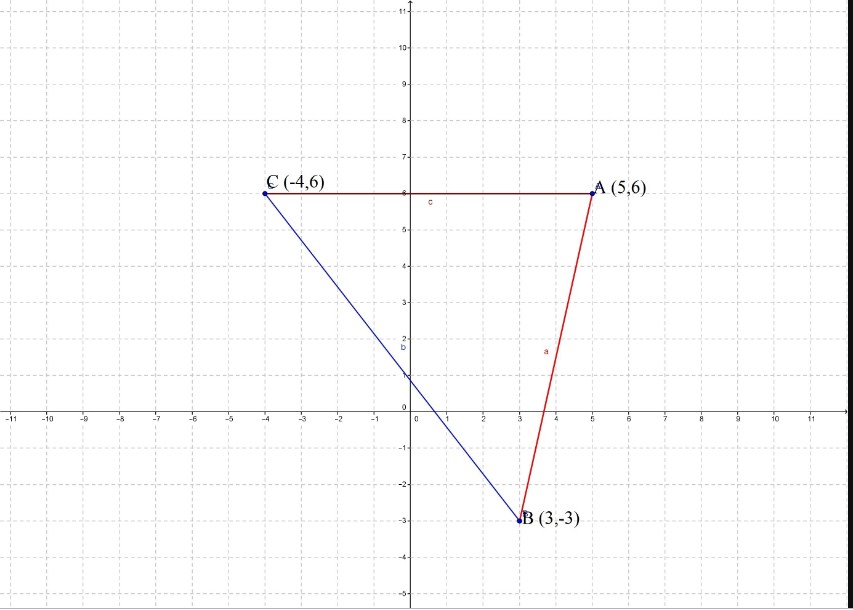
Untuk mendefinisikan koordinat diperlukan dua garis berarah yang tegak lurus satu sama lain sumbu x dan sumbu y dan panjang unit yang dibuat tanda tanda pada kedua sumbu tersebut lihat gambar 1. 0 c yakni titik potong dari sumbu y. Perhatikan gambar di bawah ini yang merupakan dua garis yang tegak lurus yaitu garis k dan i.
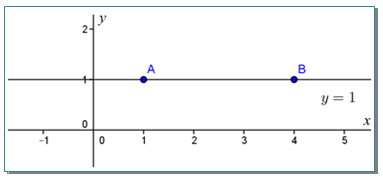
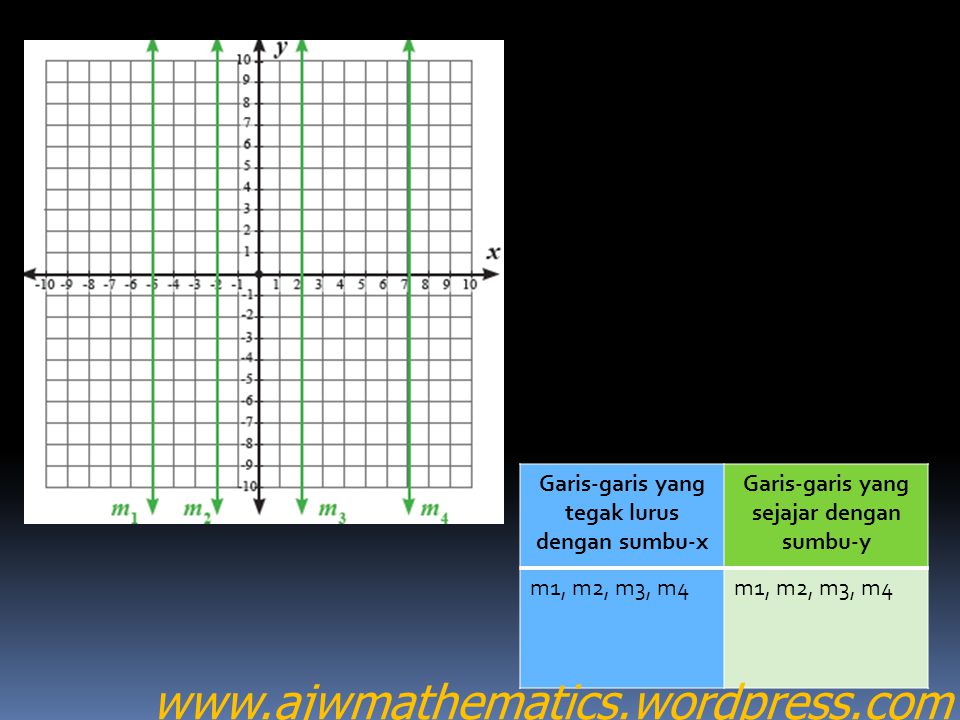
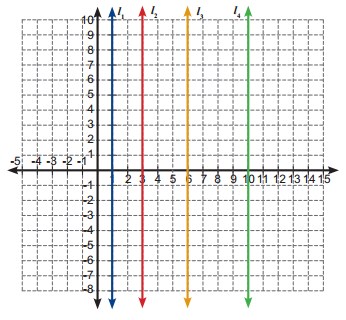
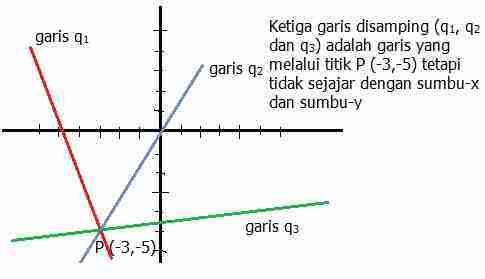
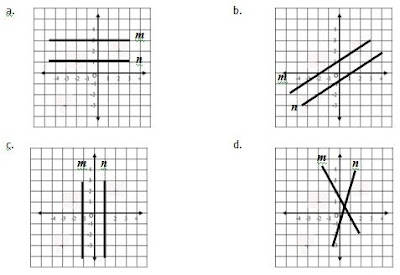
Tentukan letak koordinat titik p4 4 q7 4 r7 2 dan s4 2 pada bidang koordinat kartesius. Persamaan garis lurus bentuk umum y mx persamaan yang melalui titik pusat 0 0 dan bergradien m. Sebutkan garis garis yang tegak lurus dengan sumbu x.
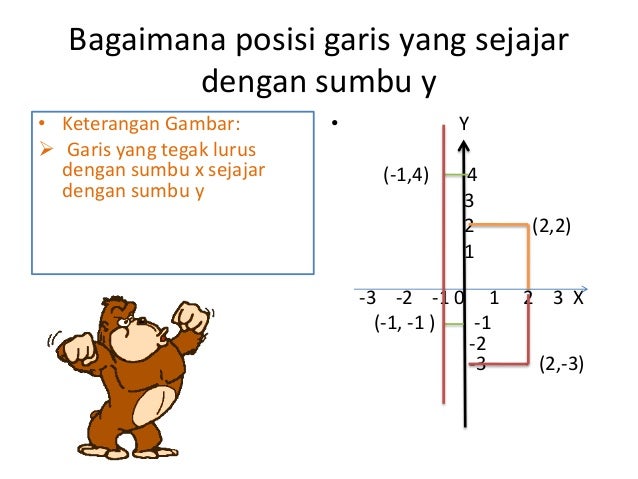
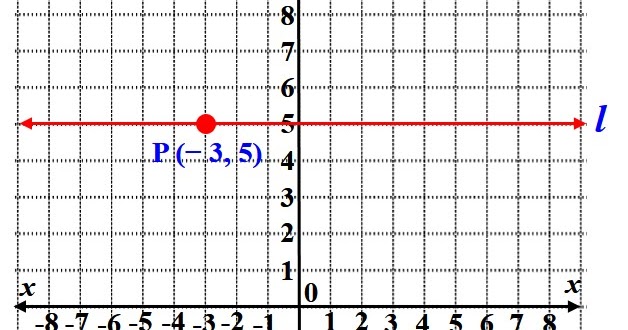
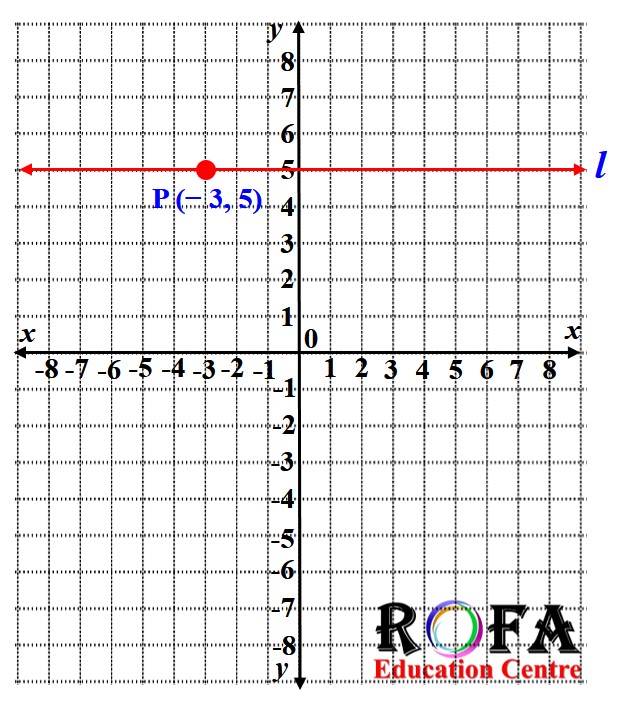
Gambarlah garis l yang tegak lurus pada sumbu x berada di sebelah kanan dan berjarak 5 satuan dari sumbu y jawab gambar garis l berupa garis tegak vertikal yang sejajar sumbu y dan memotong sumbu x secara tegak lurus di titik 5 0 dan persamaan garis l adalah x 5 2. Gradien 2 buah garis yang tegak lurus jika dikalikan hasilnya sama dengan 1. Yang dimana kedua letak dari sumbu itu ada pada satu bidang yaitu bidang xy.
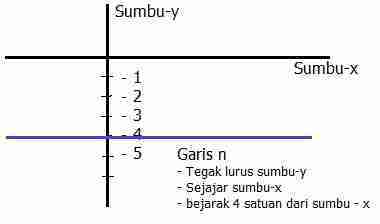
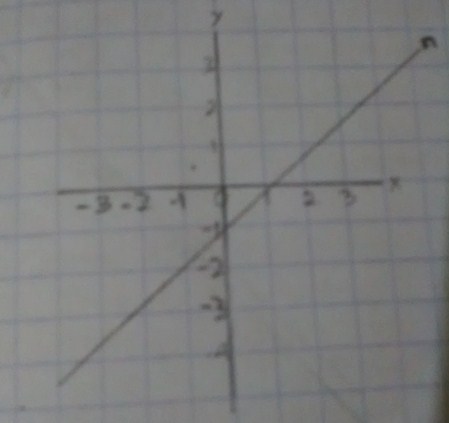
Y 2 x. Dalam matematika sistem koordinat kartesius digunakan untuk menentukan tiap titik dalam bidang dengan menggunakan dua bilangan yang biasa disebut koordinat x dan koordinat y dari titik tersebut. Gambarlah garis m yang tegak lurus pada sumbu y berada di bawah dan.
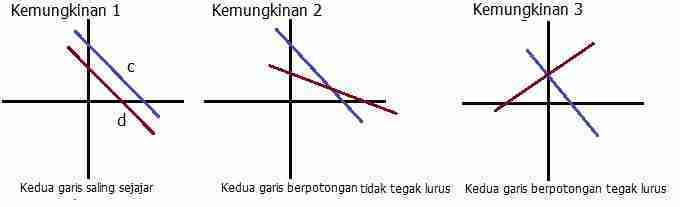
Sifat sifat garis di bidang geometri ditentukan oleh kedudukannya terhadap garis lainnya yang terdiri dari garis sejajar garis berpotongan garis tegak lurus dan garis berimpit. Sistem dari koordinat kartesius di dalam dua dimensi secara umum diartikan dengan menggunakan dua sumbu yang saling tegak lurus antara satu dengan yang lainnya. Berbeda dengan garis garis sejajar dua garis yang saling tegak lurus punya ciri yang berbeda loh.
Gradien garis yang saling tegak lurus lawan dan kebalikan m 1 atau m 1 x m 2 1. Persamaan dari garis lurus yang melewati 2 titik yakni x 1 y 1 serta x 2 y 2. Tentukan persamaan garis lurus yang melalui titik pusat 0 0 dan bergradien 2.
Y y 1 m x x 1 4. Sebutkan garis garis yang memotong dengan sumbu y. Y y 1 y 2 y 1 x x 1 x 2 x 1.
Persamaan dari garis lurus yang melewati titik nya x 1 y 1 serta bergradien m. Berikut akan dijelaskan ke 4 sifat kedudukan antar garis tersebut.

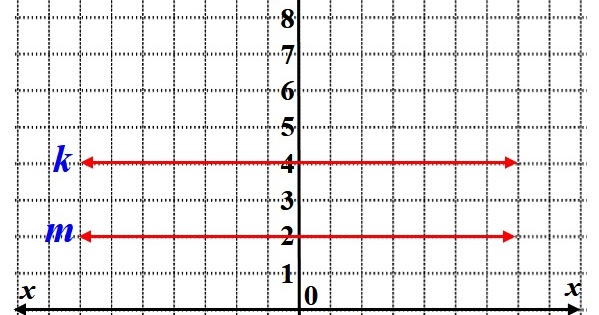
A Tentukan Garis Garis Yang Sejajar Sumbu Y Dan Tegak Lurus Sumbu X B Tentukan Garis Garis Yang Brainly Co Id
brainly.co.id
Jawaban Buku Matematika Kelas 8 Ayo Kita Berlatih 2 3 Hal 64 Gambarlah Garis L Yang Tegak Lurus Pentium Sintesi
pentiumsintesi.blogspot.com

Gambarlah Garis M Yang Tegak Lurus Sumbu Y Berada Di Bawah Dan Berjarak 4 Satuan Dari Sumbu X Youtube
m.youtube.com
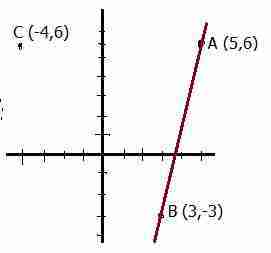
Tutorial Menjawab Soal Matematika Kelas 8 Tentang Memahami Posisi Garis Terhadap Sumbu X Dan Sumbu Y Bagian 2 Your Chemistry A
www.avkimia.com
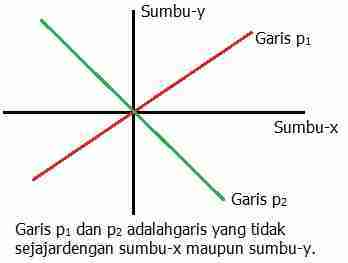
Tutorial Menjawab Soal Matematika Kelas 8 Tentang Memahami Posisi Garis Terhadap Sumbu X Dan Sumbu Y Bagian 1 Your Chemistry A
www.avkimia.com